Biomat BlogThe Original Biomat

Human Infrared and Wien's Displacement Law

Have you wondered how we can tune the Biomat's infrared energy? This article might help you understand.

Wien's Displacement Law

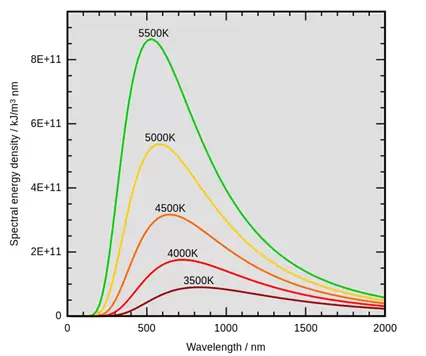
First, we need to understand that objects emit energy based on their temperature. As the temperature of the object changes, the energy peaks at different wavelengths. The shorter the wavelength, the higher the frequency. For example, a hot frying pad will emit a higher frequency than a cold one. Wien's Displacement Law tells us where that peak wavelength will be.

λmax is the wavelength at the peak energy. Notice as the temperature increases, the peak wavelength decreases.

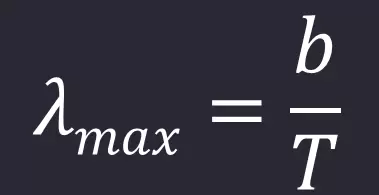
Lambda Max

The formula gives us the peak, but actually different wavelengths are emitted along a curve.

Lambda Max Curve
  • λ = Peak Wavelength
  • b = Wien's Displacement Constant
    • 2.8977729 × 10−3 m°K
    • 2,898 μm°K
  • T = Absolute temperature in Kelvin
    (Kelvin is used by scientists, where 0 is -273 °C)

The normal human body temperature is around 37 °C or 98.6 °F. We can use the equation to determine the peak wavelength. Note that this wavelength is 9.35μm. The Biomat is tuned to that frequency.

Human Infrared Calculations Tesla Infrared People

Up to 90% of human body weight comes from water, and up to 60% of the human body is water. Let's look at the absorption of energy into water by wavelength.

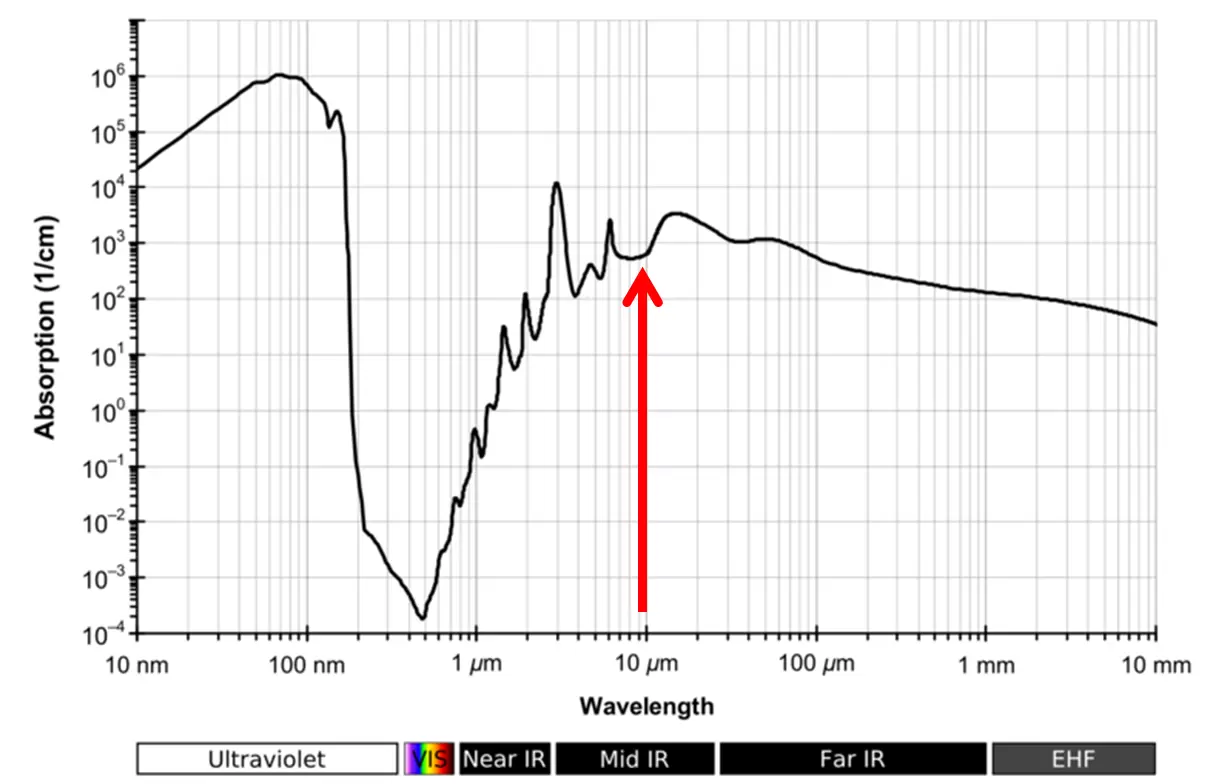
Absorption Spectrum Of Water

Note the peak near the human-infrared wavelength. Coincidence?